Today in one of my physics classes, I was explaining how to determine the voltage across and the current through resistors in a mixed series & parallel circuit: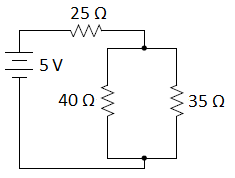
(The short summary of the process is to simplify the circuit by replacing sections with a single equivalent resistor until they can calculate the resistance of the entire circuit, then undo each step, applying Ohm’s Law at every step.)
As a way to get my students started thinking about simplifying the circuit, I decided to use a simple math problem as an analogy:
2(3 + 5) = ?
I asked them not to calculate the answer, but to explain the process of calculating the answer. Of course, the first thing a student said was “Use PEMDAS.”
I replied, “Yes. And why do we use PEMDAS?” I got the following answers:
“Because some guy said so.”
“It’s the most right way to do it.”
“So everyone does it the same.”
I asked, “Is that actually what your math teachers told you?”
“Yes. Our teachers taught us that it was so everyone does it the same way.”
So I gave them the “No, PEMDAS is not a conspiracy invented by a group of mathematicians” talk.
If you had a math problem such as:
3 + 3 + 3 + 3 + 3 + 3 + 2 + 2 + 2 + 2 + 2 + 1 =
You would group numbers together like this:
6(3) + 5(2) +1
Multiplication is just grouped addition. The reason you need to multiply before adding is because the multiplication can only group like numbers, and once you have done all of the grouping that you can (6 × 3 = 18 and 5 × 2 = 10), you still have to add the groups to each other, plus any ungrouped numbers left over.
The same is true for exponents, which are grouped multiplication. If you have:
5 · 3 · 3 · 3 · 3 · 3 · 3 · 3 · 2 · 2 · 2
You would group them as:
5 · 37 · 23
Again, you do the grouped multiplication (exponents) first, then use regular multiplication to combine the groups.
So the order of operations is: grouped multiplication, then multiplication (which is grouped addition), then addition. (Division is just multiplication by the reciprocal, so it has the same precedence as multiplication, and subtraction is just addition of a negative number, so it has the same precedence as addition.)
Parentheses exist as a way to explicitly specify a grouping other than the above.
So we use PEMDAS because that’s how the math actually works, not because a bunch of mathematicians had a council and decided how math should work. That would be like legislating the value of π. If your math teachers taught you that, they were mistaken.
At that point, one of my students quipped, “Mr. Bigler has a hit list now.”
I must respectfully disagree.
It’s not a conspiracy, but it /is/ a convention. There are other conventions–like Polish notation–that also work but aren’t as popular. Sure, the rules for multiplication over division and exponentiation over multiplication are very sensible _if you are using infix notation to do algebra_, but there’s less agreement about how multiplication and division ought to interact. And it’s not clear that doing other types of math in other notations would lead to the same conventions.
If I’m evaluating 3 + 3 + 3 + 3 + 3 + 3 + 2 + 2 + 2 + 2 + 2 + 1, I might group it as 6(3) + 5(2) + 1 as you have done. But if I’m evaluating 3 + 2 + 3 + 2 + 3 + 2 + 3 + 2 + 3 + 2 + 3 + 1, I might prefer to group it as (3+2) × 5 + 3 + 1. And if so, who is to say that 3 + 2 × 5 + 3 + 1, (left-to-right) isn’t better notation? By writing the problem one way instead of another, you have biased the discussion towards your own conclusion.
I’m not a math teacher, but I suspect that a good way to teach order of operations would be to start with none, and let the students come up with their own. Your point is that they would probably arrive at something like PEMDAS eventually, because it is a very practical and sensible convention. And I agree. But it’s not the only possible convention, nor is it /uniquely/ practical and sensible. Consider the equation “x – a × x – b = 0.” In reverse-PEMDAS (i.e. PSADME) notation, this is an already-factored quadratic whose roots are a and b. Doesn’t that seem practical and sensible?
When I was first learning the order of operations, one of the things that confused me was that it /seemed/ like PEMDAS was some occult mathematical truth, that it was a property of the operations themselves. I had a hard time making sense of what PEMDAS was trying to “tell” me. Things got easier when I realized it wasn’t trying to tell me anything; it’s just a convention. So I’m not sure that your speech will resonate with every student. For the ones for whom it doesn’t, I hope they end up reading this.
In your example of 3 + 2 + 3 + 2 + 3 + 2 + 3 + 2 + 3 + 2 + 3 + 1, grouped as (3+2) × 5 + 3 + 1, you are still doing grouped addition (5 sets of 3+2) before singleton addition.
If someone claimed that left-to-right was better, I would counter that mixing up the order in which the numbers are displayed shouldn’t change the answer.
Note also that multiplication is taught in second or third grade. At that age, groupings of 3 and separate groupings of 2 would be much easier for the kids to grasp than groupings of (3+2).
I am not a math teacher either, but it strikes me that while the left-to-right example that Marc gave might seem as valid as the PEMDAS version, it quickly breaks down when you start manipulating the numbers, as in algebra. For example, replace 2 with N. Your two options for displaying the same expression are now (left-to-right) 3 + N x 5 + 3 + 1, or (PEMDAS) (3 + N) x 5 + 3 + 1. Now say you happen to know from elsewhere that 5 x N is equal to some other value or expression that gets you closer to what you ultimately want to know; for the purpose of this discussion let’s say that 5 x N = M. If you are working with a left-to-right order of operations, clearly it would change the value to simply drop in a substitution in the middle of an expression: 3 + M + 3 + 1. How would you go about working with parts of an expression? There could be a rule that says you can only make substitutions at the beginning of an expression, but if your target is in the middle of an expression, how do you bring it to the front? Also, using PEMDAS, when faced with (3 + N) x 5 + 3 + 1, it’s clear that you can tidy up that 3 + 1, and rewrite it as (3 + N) x 5 + 4. But using left-to-right, how would you recognize and shorten bits like that? And this example is still quite straightforward compared to many in high school math class or real-world engineering and science contexts.