When potential students ask whether (high school) physics is hard, I tell them, “Imagine a year of algebra word problems, in which you have to understand a situation in order to figure out which equation to apply and how to apply it. Where most students have trouble is with the difference between understanding the problem vs. merely identifying the numbers.
Recently, I gave my students the following problem:
It’s a basic projectile motion problem, but several students had trouble with it. After a brief discussion, it turned out that the problem was that the 170.0 m given in the problem was not the distance that the projectile traveled. I asked the students who were having trouble if they had marked up the problem (either physically or in their heads) like this:
In fact, this is precisely what happened. My students did what they have been trained to do by a decade of MCAS standardized test preparation. It has worked for them because every problem they have ever encountered gave them nothing more or less than exactly what they needed to solve it.
I explained to them that they were doing something that they have been well-trained to do. However, now that they’ve passed the MCAS tests, they need to start reading the entire problem, and making decisions and assumptions based on those details that they’ve been taught to skip over. Life doesn’t give you a neat package of information when it presents you with a problem. However, in many cases, you can get enough information to solve it as long as you know what to look for.
Then I picked up a ball and threw it to one of the students in the far corner of the room. I threw it high enough to just miss the ceiling, and it came down right where the student was sitting, and he caught it easily. I asked, “How fast did I throw it?” The students looked at me blankly. Slowly and gradually, I coaxed them into figuring out what they needed to know, and how they could figure it out. When they figured out that they needed the horizontal distance, I pointed out that each of the tiles on the floor is exactly 1 ft. by 1 ft., and they could use trigonometry to figure out the horizontal distance that the ball had traveled. When they thought they needed the time that the ball was in the air, I pointed out that they could get that from the ball’s vertical motion. When they figured out that they needed the maximum height, I pointed out that the ceiling is about 12 ft. high, and the ball came within about a foot of it, so we could call the maximum height 11 ft. I also told them that they could either convert to metric units by using the approximate conversion that 1 ft. = 0.3 m, or do the problem in Imperial units by using g = 32 ft/s2.
They are used to thinking of word problems as a test to see whether they can find the right numbers and the right equation. What they need to do is to think of word problems like the ball traveling through the air: “What would I need to know in order to figure this out? Do I know any those things? Which ones can I assume?” For the seniors, I have approximately six months to undo twelve years of damage before they go to college.


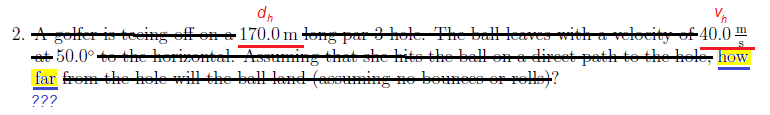
It’s worse than that. You also have to fix the teaching that proofs aren’t important because the multiple choice exams can’t test them. I find I can only repair that if students take both physics and AP chem with me. Not enough time otherwise. I found that prior to my initiating both, our kids couldn’t handle college math courses.